By the information given in the statement, you can construct the following system of equations.
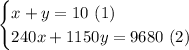
Where
x is the number of coach tickets and
y is the number of first-class tickets
To solve the system of linear equations, you can use the method of reduction or elimination, multiply the first equation by -240, add the equations and solve for the remaining variable.
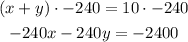
Add the equations
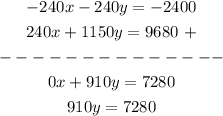
Solve for y
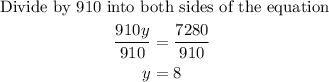
Now replace the value of y in any of the initial equations, for example in the first
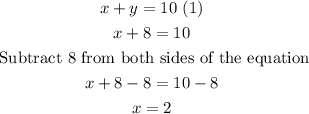
Then, the solutions of the system of linear equations are
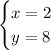
Therefore, Sara bought 8 coach tickets and 2 first-class tickets.