Question

A parabola has a vertex at (4, 0) and passes through the point (6, 1). Which of the following is the equation of this parabola in the form 2003-18-03-00-00_files/i0230000.jpg?

Answer 1

easy

y=a(x-h)^2+k
vertex is (h,k)
we know that vertex is (4,0)
input that point for (h,k)
y=a(x-4)^2+0
y=a(x-4)^2
passes thorugh the point (6,1)
input that point to find a
1=a(6-4)^2
1=a(2)^2
1=a(4)
divide both sides by 4
1/4=a

thefor the equation is
y=(1/4)(x-4)^2
or
y=(1/4)x^2-2x+4

Answer 2

The equation of this parabola in the form (A) y =
`(1)/(4)`
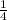
`(x-4)^(2)` .Therefore ,

(A) y =
`(1)/(4)`
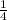
`(x-4)^(2)` is correct.

To determine the equation of the parabola in the form y= a (x-h)^{2} + k, we can use the given vertex and one additional point on the parabola.

Given that the vertex is (4, 0), the form of the parabola is y= a (x-4)^{2} + k

Now, use the point (6, 1) to solve for a and k:

1 = a(6-4)^{2} + k

1 = 4a + k

Now, we have two variables (a and k) and only one equation.

To solve for both, we need one more point on the parabola.

However, since we only have one point provided, let's use the fact that the parabola has a vertex at (4, 0).

The vertex form of a parabola is y = a (x-h)^{2} + k ,where (h,k) is the vertex.

Substitute the vertex coordinates into the equation:

0 = a (4-4)^{2} + k

0 = k

Now we can substitute k=0 back into the equation 1=4a+k:

1 = 4a + 0

Thus, a =
`(1)/(4)` .

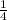Question

A parabola has a vertex at (4,0) and passes through the point (6,1). Which of the following is the equation of this parabola in the form y=a(x−h)^2 +k ?

A) y =
`(1)/(4)`
`(x-4)^(2)`

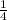
B) y =
`(1)/(2)`
`(x-4)^(2)`

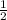
C) y =
`(3)/(4)`
`(x-4)^(2)`

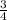
D) y =
`(x-4)^(2)`