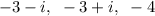Question

find all of the zeros of p(x)= x^3+10x^2+34x+40, given that -3+i is a zero. ( if there is more than one zero, separate them with commas.)

Answer 1

You have the folllowing function:

`P(x)=x^3+10x^2+34x+40`

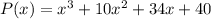
You need to remember the Conjugate zeros theorem, which states that if the polynomial function has a complex zero, then its complex conjugate is also a zero.

Knowing that the following is a zero of the function:

`-3+i`

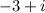
You can determine its conjugate by changing the sign in the middle of the terms. Then:

`-3-i`

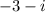
In order to find another possible zero, you can follow the steps shown below. You need to use the Rational root test. Every Rational root will have this form:

`(p)/(q)`

Where "p" is a factor of the Constant term and "q" is a factor of the Leading coefficient. Notice that the Leading coefficient is 1.

1. Find the factors of the Constant term. The possible Rational roots are:

`\pm1,\pm2,\pm4,\pm5,\pm8,\pm10,\pm20,\pm40`

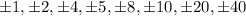
2. Substituting and evaluating, you get:

`\pm(1,2,4,5,8,10,20,40)/(1)=\pm1,\pm2,\pm4,\pm5,\pm8,\pm10,\pm20,\pm40`

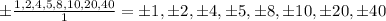
3. Substitute each value into the function and evaluate. If

`P(x)=0`

Then that value is a zero of the function.

Therefore, substituting each value into the function, you get:

`\begin{gathered} P(1)=(1)^3+10(1)^2+34(1)+40=85 \\ \\ \\ P(-1)=(-1)^3+10(-1)^2+34(-1)+40=15 \\ \\ P(2)=(2)^3+10(2)^2+34(2)+40=156 \\ \\ P(-2)=(-2)^3+10(-2)^2+34(-2)+40=4 \\ \\ P(4)=(4)^3+10(4)^2+34(4)+40=400 \\ \\ P(-4)=(-4)^3+10(-4)^2+34(-4)+40=0\text{ (This is a root)} \\ \\ P(5)=(5)^3+10(5)^2+34(5)+40=585 \\ \\ P(-5)=(-5)^3+10(-5)^2+34(-5)+40=-5 \\ \\ P(8)=(8)^3+10(8)^2+34(8)+40=1464 \\ \\ P(-8)=(-8)^3+10(-8)^2+34(-8)+40=-104 \\ \\ P(10)=(10)^3+10(10)^2+34(10)+40=2380 \\ \\ P(-10)=(-10)^3+10(-10)^2+34(-10)+40=-300 \\ \\ P(20)=(20)^3+10(20)^2+34(20)+40=12720 \\ \\ P(-20)=(-20)^3+10(-20)^2+34(-20)+40=-4640 \\ \\ P(40)=(40)^3+10(40)^2+34(40)+40=81400 \\ \\ P(-40)=(-40)^3+10(-40)^2+34(-40)+40=-49320 \end{gathered}`

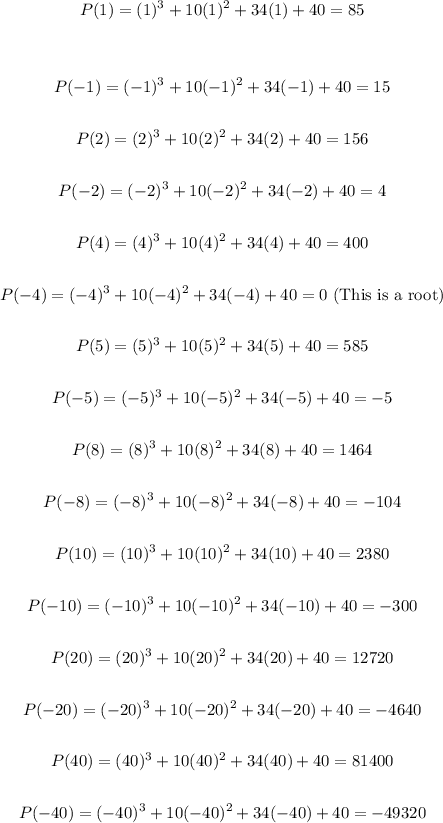
As you can notice, the other root is:

`x=-4`

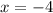
The answer is (The zeros are separated by commas):

`-3-i,\text{ }-3+i,\text{ }-4`