Question

For the following exercise, use the graph to write an equation for the function. (Please write in expanded form and factored form)

Answer 1

We are asked to determine a function that has two vertical asymptotes at:

`\begin{gathered} x=-3 \\ x=4 \end{gathered}`

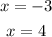
And an x-intercept at:

`x=3`

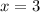
And a y-intercept at:

`y=-2`

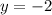
This means that the function must have the following form:

`f(x)=(k(x-x_0))/((x-a)(x-b))`

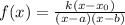
Where:

`\begin{gathered} a,b=\text{ vertical asymptotes} \\ x_0=\text{ x-intercept} \\ k=\text{ constant} \end{gathered}`

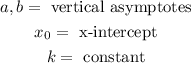
Now, we substitute the known values:

`f(x)=(k(x-3))/((x+3)(x-4))`

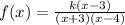
Now, we determine the value of "k" using the y-intercept, since this means that when "x = 0", then "y = -2". Substituting we get:

`-2=(k(0-3))/((0+3)(0-4))`

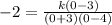
Solving the operations:

`-2=(-3k)/((3)(-4))`

Simplifying:

`-2=(-k)/(-4)`

Now, we multiply both sides by -4:

`8=-k`

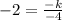
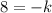
Now, we multiply both sides by -1:

`-8=k`

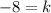
Substituting in the function we get:

`f(x)=(-8(x-3))/((x+3)(x-4))`

And thus we get the function we were looking for in the factored form.

Now, to determine the expanded form we use the distributive property on the denominator, we get:

`f(x)=(-8(x-3))/(x^2-4x+3x-12)`

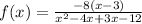
Adding like terms:

`f(x)=(-8(x-3))/(x^2-x-12)`

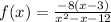
Now, we apply the distributive property on the numerator:

`f(x)=(-8x+24)/(x^2-x-12)`

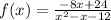
And thus we get the expanded form.