Question

The Frostburg-Truth bus travels on a straight road from Frostburg Mall to Sojourner Truth Park. The mall is 3 miles west and 2 miles south of the City Center. The park is 4 miles east and 5 miles north of the Center. How far is it from the mall to the park to the nearest tenth of a mile?

Answer 1

Let

A--------> the coordinates in a Cartesian Plane of Frostburg Mall

B--------> the coordinates in a Cartesian Plane of Sojourner Truth Park

C--------> the coordinates in a Cartesian Plane of City Center (0,0)

Step
`1`

Find the coordinates of Frostburg Mall (point A)

we know that

The mall is
`3` miles west and
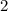`2` miles south of the City Center

so

`x\ coordinate=0-3\\ x\ coordinate=-3`

`y\ coordinate=0-2\\ x\ coordinate=-2`

Point A is equal to
`(-3,-2)`

Step
`2`

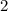
Find the coordinates of Sojourner Truth Park (point B)

we know that

The park is
`4` miles east and
`5` miles north of the City Center

so

`x\ coordinate=0+4\\ x\ coordinate=4`

`y\ coordinate=0+5\\ x\ coordinate=5`

Point B is equal to
`(4,5)`

Step
`3`

Find the distance point A and point B

`A (-3,-2)\ B (4,5)`

we know that the distance formula is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

`dAB=\sqrt{(5+2)^(2)+(4+3)^(2)}`

`dAB=\sqrt{(7)^(2)+(7)^(2)}`

`dAB=√(98)} \\ dAB=9.9\ miles`

therefore

the answer is

The distance from the mall to the park is
`9.9\ miles`

Answer 2

If we draw the distances in a Cartesian Plane, Frostburg Mall lies in the point (-3, -2) and Sojourner Truth Park is in (4, 5). Get the distance between the two points,
d = √(y2 - y1)² + √(x2 - x1)²
Substituting,
d = √(5 - -2)² + √(4 - -3)²
d = 9.90 miles
Thus, the distance between the two destinations is approximately 9.9 miles.