Answer:
ln 4768 = 5x is the logarithmic form of the equation
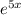 = 4768.
= 4768.
Explanation:
Given :
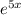 = 4768.
= 4768.
To find : What is the logarithmic form of the equation .
Solution : We have given that
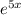 = 4768.
= 4768.
By logarithm properties :
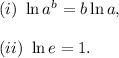 .
.
Taking logarithm both side
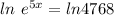
By property (1)
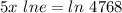 .
.
BY property (2)
5x × 1 = ln4768
5x = ln4768.
Therefore, ln 4768 = 5x is the logarithmic form of the equation
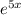 = 4768.
= 4768.