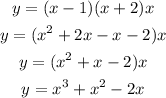Let's assume +1 and -2 refers to the ordered pairs (1, 0) and (-2, 0).
That means the cubic function has the x-intercepts at (1, 0) and (-2, 0), therefore x = 1 and x = -2 are two of the zeros of the function.
The factored form of a cubic equation is given by:
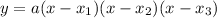
Where x1, x2 and x3 are the zeros of the function.
We have x1 = 1 and x2 = -2, so let's choose x3 = 0 and a = 1, then we have the following equation: