Question

the function f(x) = –x2 − 2x 15 is shown on the graph. what are the domain and range of the function? a. the domain is all real numbers. the range is y < 16. b. the domain is all real numbers. the range is y. c. the domain is x. the range is y. d. the domain is x. the range is y ≤ 16.

Answer 1

-x^2 - 2x + 15 = -(x^2 + 2x - 15) = -(x^2 + 2x + 1 - 15 - 1) = -(x + 1)^2 - (-15 '- 1) = -(x + 1)^2 + 16
Vertex = (-1, 16)
Range = y ≤ 16
The domain is all real numbers. the range is y

Answer 2

we have

`f(x)=-x^(2) -2x+15`

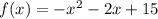
Convert to vertex form

Group terms that contain the same variable, and move the constant to the opposite side of the equation

`f(x)-15=-x^(2) -2x`

`f(x)-15=-(x^(2) +2x)`

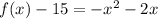
Complete the square. Remember to balance the equation by adding the same constants to each side

`f(x)-15-1=-(x^(2) +2x+1)`

`f(x)-16=-(x^(2) +2x+1)`

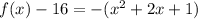
Rewrite as perfect squares

`f(x)-16=-(x+1)^(2)`

`f(x)=-(x+1)^(2)+16`

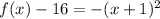
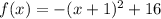
This is a vertical parabola open downward

The vertex is the point
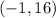`(-1,16)` is a maximun

The domain is the interval--------> (-∞,∞)

All real numbers

The range is the interval-----> (-∞,16]

`y\leq 16`

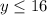
All real numbers less than or equal to
`16`

The graph in the attached figure

therefore

the answer is the option B

the domain is all real numbers. the range is y ≤ 16