The volume of a sphere is calculated as follows:
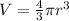
where r is the radius of the sphere.
Substituting with r = 5 cm, we get:
![\begin{gathered} V=(4)/(3)\cdot\pi\cdot5^3 \\ V=(4)/(3)\cdot\pi\cdot125 \\ V=523.3\operatorname{cm}^3 \end{gathered}]()
The volume of a right circular cone is calculated as follows:
![V=\pi r^2(h)/(3)]()
where h is the height of the cone.
Substituting with r = 5 cm, and h = 11 cm, we get:
![\begin{gathered} V=\pi\cdot5^2\cdot(11)/(3) \\ V=\pi\cdot25\cdot(11)/(3) \\ V=287.8\operatorname{cm}^3 \end{gathered}]()
The volume of the cone is less than the volume of the sphere, then the
entire volume of the frozen yogurt cannot fit completely inside the
cone.