Answer: the volume of the sample of gas at the new conditions of pressure and temperature will be 84.2 mL. The best option to answer the question is the third one (letter C, 84 mL)
Step-by-step explanation:
The question requires us to determine the volume of a sample of gas, given the following information:
Initial volume = V1 = 120.0 mL
initial pressure = P1 = 0.75 atm
initial temperature = T1 = 295 K
final volume = V2 = ?
final pressure = P2 = 1.25 atm
final temperature = T2 = 345 K
To solve this problem, we can apply the equation of ideal gases:

where P corresponds to the pressure of the gas, V is the volume of the gas, n corresponds to the number of moles of gas, R is the constant of gases and T is the temperature of the gas.
Although the conditions of pressure, volume and temperature change from the initial to the final condition, the number of moles of gas does not change. Thus, we can use the values V1, P1 and T1 given by the question to determine the number of moles of gas (n), and then use this value along with P2 and T2 to calculate the final volume (V2).
First, let's rearrange the equation of ideal gases to calculate n:

Now, let's determine n with the values given by the question (note that we won't need to give a value to R, as it will be cancelled in the following steps):

Next, we'll need to rearrange the equation of ideal gases to calculate V:
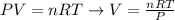
And, replacing the values of P2 and T2 given by the question, as well as the number of moles calculated, we'll have:
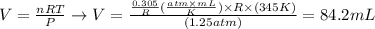
Therefore, the volume of the sample of gas at the new conditions of pressure and temperature will be 84.2 mL. The best option to answer the question is the third one (letter C, 84 mL).