Question

Under certain conditions, neon (Ne) gas diffuses at a rate of 7.0 centimeters per second. Under the same conditions, an unknown gas diffuses at a rate of 4.9 centimeters per second. What is the approximate molar mass of the unknown gas?

Answer 1

Graham's law of effusion states that the rate of effusion of two substances is equal to the square root of the reciprocal of their molar masses. Hence the equation becomes 7 / 4.9  = square root of x/ 20.18 wher e x is the molar mass of the unknown gas. The molar mass is equal to 41. 18 g/mol

Answer 2

Answer : The molar mass of unknown gas is, 41 g/mole

Solution : Given,

Diffusion rate of neon gas = 7 cm/s

Diffusion rate of unknown gas = 4.9 cm/s

Molar mass of neon gas = 20 g/mole

According to the Graham's law, the rate of effusion of a gas is inversely proportional to the square root of the molar mass of the gas.

Formula used :

`(R_1)/(R_2)=\sqrt{(M_2)/(M_1)}`

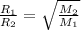
where,

`R_1` = diffusion rate of neon gas

`R_2` = diffusion rate of unknown gas

`M_1` = molar mass of neon gas

`M_2` = molar mass of unknown gas

Now put all the given values in the above formula, we get the molar mass of unknown gas.

`(7cm/s)/(4.9cm/s)=\sqrt{(M_2)/(20g/mole)}`

`M_2=40.81g/mole=41g/mole`

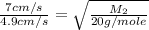
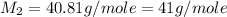
Therefore, the molar mass of unknown gas is, 41 g/mole