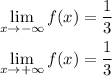Question

Can you please help me with 29Please give all forms such as limits and as_,_

Answer 1

Problem 29

We must describe the local and end behaviour of the function:

`f(x)=(2x^2-32)/(6x^2+13x-5).`

First, we rewrite the polynomials in numerator and denominator in terms of their roots:

`f(x)=(2\cdot(x^2-16))/(6\cdot(x^2+(13)/(6)x-(5)/(6)))=(1)/(3)\cdot((x-4)\cdot(x+4))/((x-(1)/(3))\cdot(x+(5)/(2)))\text{.}`

Local behaviour

We see that f(x) has a zero in the denominator for x = 1/3 and x = -5/2. The function f(x) has vertical asymptotes at these values. To analyze the local behaviour, we must compute the lateral limits for x → 1/3 and x → -5/2.

Limit x → 1/3 from the left

Computing the limit from the left when x → 1/3, is equivalent to replacing x by 1/3 - ε and computing the limit when ε → 0:

`\begin{gathered} \lim _{x\rightarrow(1)/(3)^-}f(x)=\lim _(\epsilon\rightarrow0)f((1)/(3)-\epsilon) \\ =\lim _(\epsilon\rightarrow0)(1)/(3)\cdot(((1)/(3)-\epsilon-4)\cdot((1)/(3)-\epsilon+4))/(((1)/(3)-\epsilon-(1)/(3))\cdot((1)/(3)-\epsilon+(5)/(2))) \\ =\lim _(\epsilon\rightarrow0)(1)/(3)\cdot((-(11)/(3))\cdot((13)/(3)))/((-\epsilon)\cdot((17)/(6)))\rightarrow+\infty. \end{gathered}`

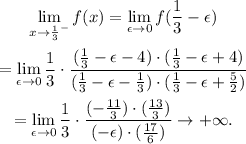
In the last step, we can't throw the ε in the parenthesis different to zero.

Limit x → 1/3 from the right

Computing the limit from the left when x → 1/3, is equivalent to replacing x by 1/3 + ε and computing the limit when ε → 0:

`\begin{gathered} \lim _{x\rightarrow(1)/(3)^+}f(x)=\lim _(\epsilon\rightarrow0)f((1)/(3)+\epsilon) \\ =\lim _(\epsilon\rightarrow0)(1)/(3)\cdot(((1)/(3)+\epsilon-4)\cdot((1)/(3)+\epsilon+4))/(((1)/(3)+\epsilon-(1)/(3))\cdot((1)/(3)+\epsilon+(5)/(2))) \\ =\lim _(\epsilon\rightarrow0)(1)/(3)\cdot((-(11)/(3))\cdot((13)/(3)))/((+\epsilon)\cdot((17)/(6)))\rightarrow-\infty. \end{gathered}`

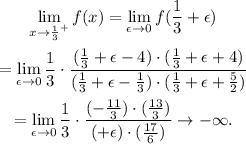
In the last step, we can't throw the ε in the parenthesis different to zero.

Limit x → -5/2 from the left

Computing the limit from the left when x → -5/2, is equivalent to replacing x by -5/2 - ε and computing the limit when ε → 0:

`\begin{gathered} \lim _{x\rightarrow-(5)/(2)^-}f(x)=\lim _(\epsilon\rightarrow0)f(-(5)/(2)-\epsilon) \\ =\lim _(\epsilon\rightarrow0)(1)/(3)\cdot((-(5)/(2)-\epsilon-4)\cdot(-(5)/(2)-\epsilon+4))/((-(5)/(2)-\epsilon-(1)/(3))\cdot(-(5)/(2)-\epsilon+(5)/(2))) \\ =\lim _(\epsilon\rightarrow0)(1)/(3)\cdot((-(13)/(2))\cdot((3)/(2)))/((-(17)/(6))\cdot(-\epsilon))\rightarrow-\infty. \end{gathered}`

In the last step, we can't throw the ε in the parenthesis different to zero.

Limit x → -5/2 from the right

Computing the limit from the left when x → -5/2, is equivalent to replacing x by -5/2 + ε and computing the limit when ε → 0:

`\begin{gathered} \lim _{x\rightarrow-(5)/(2)^+}f(x)=\lim _(\epsilon\rightarrow0)f(-(5)/(2)+\epsilon) \\ =\lim _(\epsilon\rightarrow0)(1)/(3)\cdot((-(5)/(2)+\epsilon-4)\cdot(-(5)/(2)+\epsilon+4))/((-(5)/(2)+\epsilon-(1)/(3))\cdot(-(5)/(2)+\epsilon+(5)/(2))) \\ =\lim _(\epsilon\rightarrow0)(1)/(3)\cdot((-(13)/(2))\cdot((3)/(2)))/((-(17)/(6))\cdot(+\epsilon))\rightarrow+\infty. \end{gathered}`

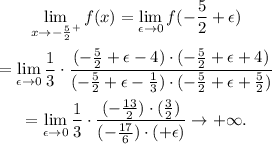
In the last step, we can't throw the ε in the parenthesis different to zero.

End behaviour

To describe the end behaviour of the function, we must compute the limits of the function when x → -∞ and x → +∞.

Limit x → -∞

`\lim _(x\rightarrow-\infty)f(x)=\lim _(x\rightarrow-\infty)(2x^2-32)/(6x^2+13x-5)=(\lim_(x\rightarrow-\infty)(2x^2-32)/(x^2))/(\lim_(x\rightarrow-\infty)(6x^2+13x-5)/(x^2))=(2)/(6)=(1)/(3)\text{.}`

To compute the limit we have divided numerator and denominator by x² and distributed the limit. The result of each limit is given by the leading term, which has the highest power of x.

Limit x → +∞

`\lim _(x\rightarrow+\infty)f(x)=\lim _(x\rightarrow+\infty)(2x^2-32)/(6x^2+13x-5)=(\lim_(x\rightarrow+\infty)(2x^2-32)/(x^2))/(\lim_(x\rightarrow+\infty)(6x^2+13x-5)/(x^2))=(2)/(6)=(1)/(3)\text{.}`

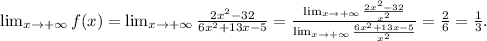
To compute the limit we have divided numerator and denominator by x² and distributed the limit. The result of each limit is given by the leading term, which has the highest power of x.

Answers

Local behaviour

The function f(x) has vertical asymptotes at x = 1/3 and x = -5/2.

`\begin{gathered} \lim _{x\rightarrow-(1)/(3)^-}f(x)=+\infty \\ \lim _{x\rightarrow-(1)/(3)^+}f(x)=-\infty \\ \lim _{x\rightarrow-(5)/(2)^-}f(x)=-\infty \\ \lim _{x\rightarrow-(5)/(2)^+}f(x)=+\infty \end{gathered}`

End behaviour

`\begin{gathered} \lim _(x\rightarrow-\infty)f(x)=(1)/(3) \\ \lim _(x\rightarrow+\infty)f(x)=(1)/(3) \end{gathered}`