Question

A mechanic uses a hydraulic lift to raise a car above her head. The car weighs 22,500N, and is raised by a piston with a 30cm diameter. What is the diameter of the smaller piston, if the force acting on it is 1500 N

Answer 1

First, take into account that the pressure on each piston must be equal:

`P_1=P_2`

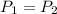
then, by conisdering that P=F/A, you have:

`(F_1)/(A_1)=(F_2)/(A_2)`

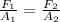
furthermore, consider that the area of the piston (circular shape) is:

`A=\pi r^2`

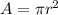
then, in order to determine the diameter of the smaller piston, replace the previous expression into the equation for F/A, and solve it for r2, just as follow:

`\begin{gathered} (F_1)/(\pi r^2_1)=(F_2)/(\pi r^2_2) \\ r_2=\sqrt[]{(F_2)/(F_1)r^2_1}^{} \end{gathered}`

take into account that the radius of the bigger piston is

r1=d1/2=30cm/2 = 15cm,

then by replacing F1 = 22,500N and F2=1,500N, you obtain for r2:

the diameter of the smaller piston is twice its radius, then, you have:

d2 = 2*r2 = 2*(3.87 cm) = 7.74 cm