Answer: The correct option is (D) 19.
Step-by-step explanation: Given that the map of a biking trail is drawn on a coordinate grid.
The trail starts at P(−6, 3) and goes to Q(3, 3). It goes from Q to R(3, −4) and then to S(6, −4).
We are to find the total length in units of the biking trail.
The length of a line segment is equal to the distance between the endpoints of the segment.
Distance formula :
The distance between two points (a, b) and (c, d) is given by
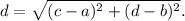
So, the length of the line segments PQ, QR and RS are given by
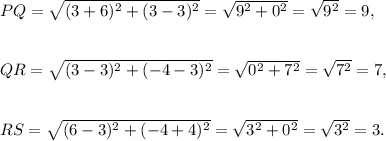
Therefore, the total length of the biking trail is given by
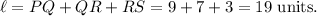
Thus, the total length of the biking trail is 19 units.
Option (D) is CORRECT.