Since whether they had a boy or a girl in each birth is independent in each of them we have independent events. This means that we can use the binomial distribution to solve this problem, the binomial distribution is given by:

where n is the number of trials, k is the number of successes and p is the probability of success. For this problem the number of trials is 9 and the probability of succes is 0.5
Probability of having at least 2 girls:
In this case we need the probability:
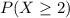
To find it we would need to add the probability of getting 2, 3, 4 and so on until 9. To simplify teh calculation we can use the fact that:
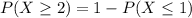
which comes from the fact that the sum of the probability of all the posibilities has to be equal to 1, then we have:
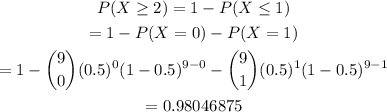
Therefore, the probability of getting at least two girls is 0.98046875
Probability of having at most 4 girls:
In this case we have:

Therefore, the probaility of having at most 4 girls is 0.5