Question

Determine an equation of the line which is the perpendicular bisector of the segment whose endpoints arp (-5,3) and (7.2). Make sure to show all work.

Answer 1

The given points are (-5,3), and (7,2).

First, we have to find the slope of the line that passes through the given points.

`m=(y_2-y_1)/(x_2-x_1)`

Replacing the given points, we have

`m=(2-3)/(7-(-5))=(-1)/(7+5)=-(1)/(12)`

Since we have to find a perpendicular bisector to the line that passe through the given points, we have to find the perpendicular slope to -1/12.

`m_1\cdot m=-1`

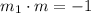
Replacing the slope, we have

`\begin{gathered} m_1\cdot(-(1)/(12))=-1 \\ m_1=12 \end{gathered}`

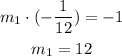
So, the perpendicular bisector has a slope of 12.

Additionally, a perpendicular bisect passes through the midpoint between (-5,3) and (7,2), so let's find it

`\begin{gathered} M=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ M=((-5+7)/(2),(3+2)/(2)) \\ M=((2)/(2),(5)/(2)) \\ M=(1,(5)/(2)) \end{gathered}`

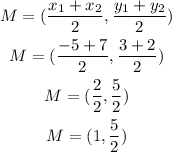
Now, we use this midpoint, the slope, and the point-slope formula to find the equation of the perpendicular bisector

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(5)/(2)=12(x-1) \\ y=12x-12+(5)/(2) \\ y=12x-(24+5)/(2) \\ y=12x-(29)/(2) \end{gathered}`

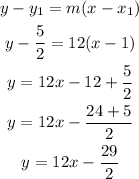
Therefore, the equation of the perpendicular bisector is

`y=12x-(29)/(2)`