Question

1. Find what price maximizes profits.

Starting Cost: 700,000
Cost per unit: 110
Demand Curve: 70,000 - 200P

Answer 1

The price that maximizes profits is $230 per good

The maximum profits earned at the above set price is $2,180,000

Explanation:

Determine the profit function

`Q=70000-200P\\Q+200P=70000\\200P=70000-Q\\P=350-(1)/(200)Q`

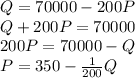
Find the total revenue function

`TR=P*Q\\TR=(350-0.005Q)*Q\\TR=350Q-0.005Q^2`

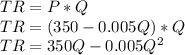
Find the total profit function

`TP=TR-TC\\TP=(350Q-0.005Q^2)-(110Q+700000)\\TP=240Q-0.005Q^2-700000`

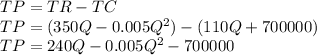
Determine the profit-maximizing quantity of output

`(d(PT))/(dQ)=240-0.01Q`

`0=240-0.01Q`

`-240=-0.01Q`

`24000=Q`

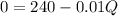
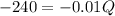
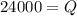
Determine the profit-maximizing price

`P=350-0.005Q\\P=350-0.005(24000)\\P=350-120\\P=230`

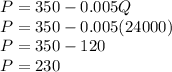
(Optional) Determine the total profit

`TP=240Q-0.005Q^2-700000\\TP=240(24000)-0.005(24000)^2-700000\\TP=2180000`

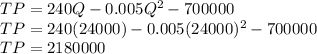
This means that the firm makes its maximum profit of $2,180,000 when the price per good is set to $230.