Answer:
The radius of the circle is 17 units. The point (-15,-16) or (-15,14) lies on this circle.
Explanation:
It is given that the circle is centered at the point (-7, -1) and passes through the point (8, 7).
Distance formula:

Using distance formula we get,
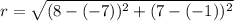
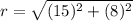
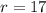
The radius of the circle is 17 units.
Let the circle passing through the point (-15,y).
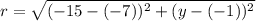
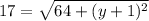
Taking square root both the sides.
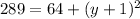
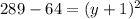

Taking square root both the sides.
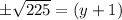
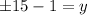

The value of y is either -16 or 14.
Therefore the radius of the circle is 17 units. The point (-15,-16) or (-15,14) lies on this circle.