Question

which are the roots of the quadratic function f(b) = b2 – 75? check all that apply. b = 5 square root of 3 b = -5 square root of 3 b = 3 square root of 5 b = -3 square root of 5 b = 25 square root of 3 b = -25 square root of 3

Answer 1

`b=5√(3)` and
`b=-5√(3)` are the roots of given quadratic equation.

Explanation:

Given quadratic equation is
`f(b)=b^2-75`

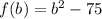
We have to check all the given options.

If the value of f(b) gives 0 when put the value of b in above equation then only that b value is the root of quadratic equation.

`b=5√(3): (5√(3))^(2)-75=75-75=0`

`b=-5√(3): (-5√(3))^(2)-75=75-75=0`

`b=3√(5): (3√(5))^(2)-75=45-75=30\\eq 0`

`b=-3√(5): (-3√(5))^(2)-75=45-75=30\\eq 0`

`b=25√(3): (25√(3))^(2)-75=1875-75=1800\\eq 0`

`b=-25√(3): (-25√(3))^(2)-75=1875-75=1800\\eq 0`

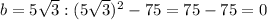
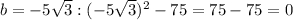
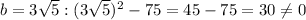
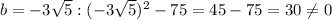
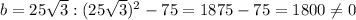
hence, only first two values
`b=5√(3),-5√(3)` gives the value of f(b)=0 .

⇒
`b=5√(3)` and
`b=-5√(3)` are the roots of given quadratic equation.

Answer 2

The answers are b = 5 square root of 3; b = -5 square root of 3. f(b) = b^2 – 75. If f(b) = 0, then b^2 – 75 ) 0. b^2 = 75. b = √75. b = √(25 * 3). b = √25 * √3. b = √(5^2) * √3. Since √x is either -x or x, then √25 = √(5^2) is either -5 or 5. Therefore. b = -5√3 or b = 5√3.