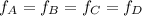Given:
Cross-sectional area of the pipe at C is half that at A.
Cross-section area at A = Cross sectional area at D.
Water flows in from right to left.
Let's determine which of the following correctly ranks the mass flow rate in sections A, B, C, and D.
According to Bernoulli's principle:
Mass flow rate = density x volume of flow rate.
Where:
Volume of flow rate = (cross sectional area) x (velocity).
Now, to apply the volume flow rate in different sections of the pipe, we have:
Volume flow rate = A*V = constant.
The volume flow rate is constant, according to the equation of continuity.
Now, the equation of continuity is:
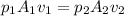
This means the rate of mass flow in all sections will be equal.
Therefore, the correct ranking of the mass flow rate of the four sections are:
fA = fB = fC = fD
ANSWER: D.