The sum of the probabilities is always equal to 1. Summing up the probabilities given on the data set, we have
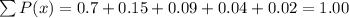
Given the probability distribution table, the mean number per inning can be computed as
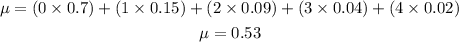
For the computation of the standard deviation, we need to solve first for the square of the difference of the number of innings on the mean. We have the following
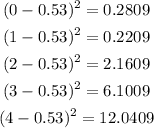
We then multiply these values on the corresponding probability of each inning given in the probability distribution table. We have
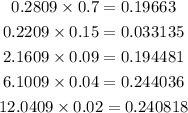
We now get the sum of the values computed above and get the square of it.
![\begin{gathered} 0.19663+0.033135+0.194481+0.244036+0.240818 \\ \sigma=\text{ }\sqrt[]{0.9091}=0.953 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ffq88symjdq5ylcc84am.png)