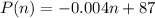Question

A clothing business finds there is alinear relationship between the numberof Shirts, n it Can Sell and thePrice, P, it canCharge per Shirt.In particular, huforical data showsthat 3 thousand shirts can be soldat a price of $78 each, and that 7thousand Shirts can be sold at a price $62 eachEquation form P(n)=mn+b

Answer 1

We are looking for the linear equation P(n) = mn + b where n is equal to the number of shirts sold and P(n) is the price per shirt.

We know that if n = 3,000, P(n) = 78, and if n = 7,000. P(n) = 62. We can write these in quation form (using P(n) = mn +b):

`\begin{gathered} 78=3,000m+b \\ 62=7,000m+b \end{gathered}`

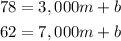
We can then use the substitution method to solve for m and b. Let's use 78 = 3,000m + b to express b.

`\begin{gathered} 78=3,000m+b \\ 78-3,000m=b \end{gathered}`

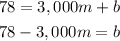
We'll then substitute this in 62 = 7,000m + b.

`\begin{gathered} 62=7,000m+b \\ 62=7,000m+(78-3,000m) \\ 62-78=7,000m-3,000m \\ -16=4,000m \\ m=-(16)/(4,000)=-0.004 \end{gathered}`

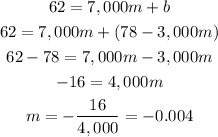
Then we can use m = -0.004 to solve for b.

`\begin{gathered} b=78-3,000b \\ b=78-3,000(-0.004) \\ b=75+12 \\ b=87 \end{gathered}`

We now have the complete equation for P(n):

`P(n)=-0.004n+87`