Question

the length of the rectangle is two feet less than 3 times the width.if the area is 65ft^2.findvthe dimensuon.

Answer 1

Let the length be x and the width be y.

As per the first condition:

`x=3y-2\ldots(i)`

As per the second condition, the area is 65 sq feet so it follows:

`xy=65\ldots(ii)`

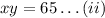
Substitute the value of x obtained from (i) in (ii) and solve for y as follows:

`\begin{gathered} y(3y-2)=65 \\ 3y^2-2y=65 \\ 3y^2-2y-65=0 \end{gathered}`

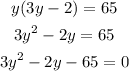
Solve the quadratic as follows:

`\begin{gathered} 3y^2-15y+13y-65=0 \\ 3y(y-5)+13(y-5)=0 \\ (y-5)(3y+13)=0 \\ y=5,-(13)/(3) \end{gathered}`

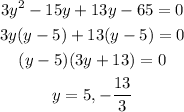
Since the width is never negative, y=5, therefore solve for x from (i) to get:

`x=3(5)-2=13`

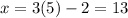
Hence the length is 13 feet and the width is 5 feet.