Question

Suppose you have two similar rectangular prisms. The volume of the smaller rectangular prism is 64 in^3 and the volume of the larger rectangular prism is 1331 in^3. What is the scale factor of the smaller figure to the larger figure?A) 4:11B) 1:21C) 3:10D) 9:25

Answer 1

Answer:

The scale factor of the smaller figure to the larger figure is 4:11 (option A)

Step-by-step explanation:

Given:

The volume of the smaller rectangular prism = 64 in^3

The volume of a larger rectangular prism = 1331 in^3

The prisms are similar

To find:

the scale factor of the smaller figure to the larger figure

For similar shapes, the scale factor of the shapes when the volumes are given:

`\frac{Volume\text{ of the smaller figure}}{Volume\text{ of the larger figure}}\text{ = \lparen scale factor\rparen}^3`
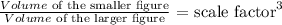
`\begin{gathered} (64)/(1331)\text{ = \lparen scale factor\rparen}^3 \\ \\ cube\text{ root both sides:} \\ \sqrt[3]{(64)/(1331)}\text{ = }\sqrt[3]{(scale\text{ factor\rparen}^3} \\ \\ \sqrt[3]{(4^3)/(11^3)}\text{ = }\sqrt[3]{(scale\text{ factor\rparen}^3} \\ \\ (4)/(11)\text{ = scale factor} \end{gathered}`

The scale factor of the smaller figure to the larger figure is 4:11 (option A)