Question

We often use Z scores to compare values.SAT-Math scores are normally distributed with a mean of 500 and standard deviation of 100. ACT-Math scores are normally distributed with a mean of 18 and standarddeviation of 6. A student has taken both tests. They scored 600 on the SAT-Math and 22 on the ACT-Math. Which score is more impressive?Record a Response

Answer 1

To answer this question, we need to use the formula for z-scores, a standardized value used in the standard normal distribution. The formula for that is as follows:

`z=(x-\mu)/(\sigma)`

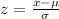
We have to use, in both cases, the corresponding mean, standard deviation, and the raw score, x.

First Case: SAT Math Scores

• Mean (mu) = 500.

,

• Standard deviation (sigma) = 100.

,

• Raw score (x) = 600

Then, we have:

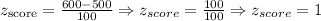
`z_{\text{score}}=(600-500)/(100)\Rightarrow z_(score)=(100)/(100)\Rightarrow z_(score)=1`Second Case: ACT Math Scores

• Mean (mu) = 18

,

• Standard deviation (sigma) = 6

,

• Raw score (x) = 22

Therefore:

`z_{\text{score}}=(22-18)/(6)\Rightarrow z_(score)=(4)/(6)\Rightarrow z_(score)=0.666666\approx0.67`

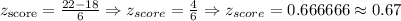
Now, with these two values for z, we can use the cumulative standard normal distribution to see the percentiles of this z_scores:

• For z_score = 1, we have that: ,0.84134 (approximately)

,

• For z_score = 0.67, we have that:, 0.74857 (approximately)

Conclusion: We have, then, that the more impressive score is the one obtained at SAT-Math since the value is for z = 1, and this value is more to the right than that one of z = 0.67 obtained at ACT Math. In fact, the value obtained at SAT-Math is, approximately, above 84% of the values for the population, while that one obtained at ACT-Math is only almost 75% above the values for the population.