So the table has two missing values: one for x=-2 and another for x=3. In order to fill them we must replace the corresponding x value in the equation. Then we get:
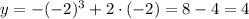
So the y value below x=-2 is 4.
For the other blank space we get:

So the y value below x=3 is -21. And those are the answers to part (a).
In part b we need to draw rhe graph of the function between x=-2.3 and x=3.5. We need to use a scale of 2 cm to 1 unit in the x-axis and 2 cm to 5 in the y-axis. This basically means that the distance between consecutive units (between 1 and 2, between 2 and 3,...) in the x-axis must be 2cm. The distance between consecutive units in the y-axis can be calculated:
![\frac{2\operatorname{cm}}{5\text{unit}}=0.4\frac{\operatorname{cm}}{\text{unit}}]()
So the distance between two consecutive units in the y-axis must be 0.4 cm. With these distances you can draw the grid. Once you have the grid you simply need to draw the points given by table 2. Then guiding yourself with those points you can draw the entire graph of the function. You'll end with something like this:
And that's the answer to part (b).
In part (c) we must find y when x=-19 and x when y=-7. For the first we can use the equation. First we replace x with -19 and find y:

For the second we can use the graph. We draw an horizontal line (in blue) that passes through y=-7. Then we mark the point (in gray) where this line meets the green graph. From that point we can draw a vertical line (in red) that has to intercept the x-axis. The point where they meet give us an approximate value of x. You should end with something like this:
As you can see the red line meets the x-axis in the midpoint between 2 and 2.5. This value is 2.25 so we have x=2.25.
Then the answer to part (c) (i) is y=6821.
The answer to part (c) (ii) is x=2.25.