The distance travelled by Carol is given by the product between the time she travelled and the rate she rides. The same logic is applied to Harry.
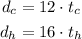
If we use our time variables using hour as the unit, let's start by converting the time difference between their departure to hours.
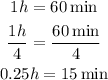
The difference between their departure is 0.25h. Since Harry departed later, the total time travelled by Carol when Harry catch up is the time Harry travelled plus 0.25h.
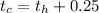
Renaming the time travelled by Harry as t, our initial equations turns out to be
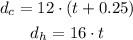
When Harry catch up, the distance travelled by them will be the same, therefore
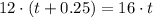
Solving for t, we have
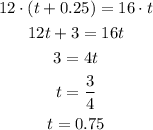
Now we know that Harry catch up with carol after 0.75h(45 minutes). Plugging this value in our expression, we have
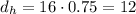
Harry travelled 12 miles to catch up with Carol.