Question

I f x ≠ – 2 a n d x ≠ 32 , w h a t i s t h e s o l u t i o n t o

Answer 1

`x=5,x=3`

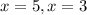
1) The restraint that x ≠2 and x≠3/2 is the condition that prevents that to have a zero on the denominator. 0 on the denominator makes an undefinition.

2) So now, let's solve it:

`\begin{gathered} (5)/(x+2)=(x)/(2x-3) \\ 5(2x-3)=x(x+2) \\ 10x-15=x^2+2x \\ -x^2+10x-2x-15=0 \\ -x^2+8x-15=0 \\ x^2-8x+15=0 \end{gathered}`

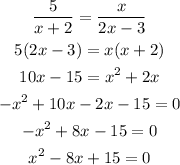
Note that cross multiplying we get a quadratic equation. So let's solve it:

`\begin{gathered} x^2-8x+15=0 \\ Sx=-5-3=8_{}_{}_{} \\ Px=-5\cdot-3=15 \end{gathered}`

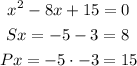
Note that the sum of two numbers that yield -8x is -5 and -3 as well as -5 x -3 yields 15 as their product. But to find the answers via this method, we need to switch signs, so the answer is:

`x_1=5,x_2=3`

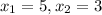
A quadratic equation yields two roots. And that's the answer.