Question

Consider the functions f(x) = 2x + 1 and g(x) = x2 − 10. What is the value of f[g(3)]?

39
−3
−7
−1

Answer 1

f(x)=2x +1
g(X)=x^2 -10

g(3)=9-10 = - 1

f(g(3)) =f(-1)=2*(-1) +1 = - 2 +1 = - 1

so the last one choice is right sure

Answer 2

Option (d) is correct.

`f[g(3)]=-1`

Explanation:

Given :
`f(x)=2x+1` and
`g(x)=x^2-10`

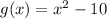
We have to find the value of
`f[g(3)]`

Since, we have to calculate
`f[g(3)]`

`f[g(3)]` represents a composition of function f(x) and g(x)

We first find g(3) that is value of g at x = 3

Substitute x = 3 in g(x), we have,

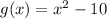`g(x)=x^2-10` thus, at x = 3 , we have

`g(3)=3^2-10=9-10=-1`

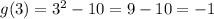
now,
`f[g(3)]` becomes
`f[-1]`

Thus, now we calculate f(x) at x = -1

thus we have,

`f(x)=2x+1` at x = -1 , we have,

`f(-1)=2(-1)+1=-2+1=-1`

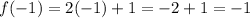
Thus,
`f[g(3)]=-1`

Option (d) is correct.