Question

Select the correct answer.What are the zeros of the function y= (x - 4)(x7 - 12x+ 36)?

Answer 1

B. 4 and 6

Step-by-step explanation

The function is partially factored. As we can see, one of the factors is (x - 4), which means that x = 4 is one of the three zeros this function has.

The other two zeros are the zeros of the factor (x² - 12x + 36), so we have to solve,

`x^2-12x+36=0`

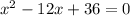
To solve it, we can use the quadratic formula,

`\begin{gathered} ax^2+bx+c=0 \\ \\ x=(-b\pm√(b^2-4ac))/(2a) \end{gathered}`

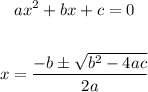
In this case, a = 1, b = -12, and c = 36,

`x=(-(-12)\pm√((-12)^2-4\cdot1\cdot36))/(2\cdot1)=(12\pm√(144-144))/(2)=(12\pm0)/(2)=(12)/(2)=6`

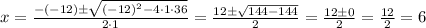
We should have got two zeros, but we only got one since the discriminant is 0. This means that this zero has multiplicity 2.

Hence, the zeros of this function are 4 and 6.