Question

A ball is thrown vertically upward. After t seconds, its height h (in feet) is given by the function h (t) = 56t - 167. What is the maximum height that the bawill reach?Do not round your answerх$?A

Answer 1

Write out the function given in the question

`h(t)=56t-16t^2`

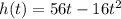
Note that at the maximum height the derivative of the function would be equal to zero

Find the derivative of the function using the formula

`\begin{gathered} \frac{dh}{\text{ dt}}=ant^(n-1) \\ \frac{dh}{\text{ dt}}=56*1t^(1-1)-16*2t^(2-1) \\ =56-32t \end{gathered}`

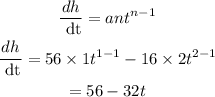
Equate the derivative to zero to get the value of t because the derivative is zero at maximum height

`\begin{gathered} 56-32t=0 \\ 56=32t \\ 32t=56 \\ t=(56)/(32) \\ t=(7)/(4) \end{gathered}`

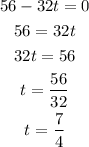
Substitute the value of t into the function

`\begin{gathered} h(t)=56t-16t^2 \\ \text{when t=7/4} \\ h((7)/(4))=56((7)/(4))-16((7)/(4))^2 \end{gathered}`
`\begin{gathered} h((7)/(4))=14*7-16((49)/(16)) \\ =98-49=49\text{ feet} \end{gathered}`

Hence, the maximum height that the ball will reach is 49feet