Question

2. Create an equation that represents the table from Question #1 (FLE.2)

Answer 1

`\begin{gathered} \text{ Computer} \\ y=-185x+960 \\ \text{ Printer} \\ y=-60x+300 \end{gathered}`

Explanation:

We have that the equation in its slope and intercept form is the following:

`\begin{gathered} y=mx+b \\ \text{where m is the slope and b is y-intercept} \end{gathered}`

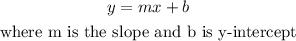
We calculate the slope as follows:

`m=(y_2-y_1)/(x_2-x_1)`

We calculate the slope for the computer value and for the printer value:

In the computer value, we have the points (0, 960) and (3, 405), replacing:

`\begin{gathered} m=(405-960)/(3-0) \\ m=-185 \end{gathered}`

In the printer value, we have the points (0, 300) and (3, 120), replacing:

`\begin{gathered} m=(120-300)/(3-0) \\ m=-60 \end{gathered}`

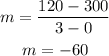
The intercept with b is the point when x is equal to 0, therefore, the two equations would be:

The equation for the value of computer:

`y=-185x+960`

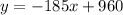
The equation for the value of printer:

`y=-60x+300`