Question

Lucky Dog Daycare will be enclosing an 800 square feet outdoor area. One side will be formed by the external wall of their building, two sides will be constructed of pine boards, and the fourth side will be made of galvanized steel fencing. If the pine board fencing costs $6/running foot and the steel fencing costs $2/running foot, determine the dimensions of the enclosure that can be erected at a minimum cost.

Answer 1

From the question, let the

Length of pine boards be represented as x and

Let the length of galvanized steel fencing be represented as y.

The diagram of Lucy Dog Daycare can be represented as follows

So, the Total cost C should include cost of two pine boards 2x and cost of one galvanized steel y. So we have

`C=2x(6)+y(2)`

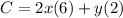
So, we have

`\begin{gathered} C=2x(6)+y(2) \\ C=12x+2y \end{gathered}`

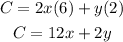
Also the total area is 800 square. That is

`\begin{gathered} x* y=800 \\ xy=800 \\ y=(800)/(x) \end{gathered}`

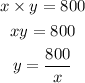
Now substituting the value of y into the cost equation, we have

`\begin{gathered} C=12x+2y \\ C=12x+2*(800)/(x) \\ C=12x+(1600)/(x) \end{gathered}`

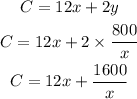
Taking the derivative, we have

`\begin{gathered} (dC)/(dx)=12+(-(1600)/(x^2) \\ (dC)/(dx)=12-(1600)/(x^2) \end{gathered}`

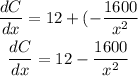
At minimum or maximum cost, the derivative should be equal to zero,

So

`\begin{gathered} 12-(1600)/(x^2)=0 \\ 12=(1600)/(x^2) \\ 12x^2=1600 \\ x^2=(1600)/(12) \\ x^2=133.333333 \\ x=√(133.33333) \\ x=11.5470053 \end{gathered}`

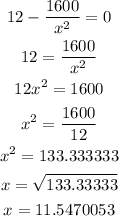
Hence x = 11.55 ft

From the equation above, where y was made the subject, we have

`\begin{gathered} y=(800)/(11.5470053) \\ y=69.28203 \end{gathered}`

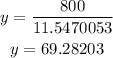
Hence y = 69.28 ft

Hence the dimensions that could be used at a minimum cost is 11.55 ft of pine boards by 69.28 ft of galvanized steel