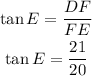Question

Use the Pythagorean Theorem to find the missing leg of the right triangle and the. Identify the trig ratios

Answer 1

The Pythagorean theorem states:

`c^2=a^2+b^2`

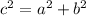
where a and b are the legs and c is the hypotenuse of a right triangle.

In triangle EDF, DE = 29 is the hypotenuse, and FE = 20 and DF are the legs. Substituting this information into the formula and solving for DF, we get:

`\begin{gathered} DE^2=FE^2+DF^2 \\ 29^2=20^2+DF^2 \\ 841=400+DF^2 \\ 841-400=DF^2 \\ \sqrt[]{441}=DF \\ 21=DF \end{gathered}`

Sine formula

`\sin (angle)=\frac{\text{opposite side}}{hypotenuse}`

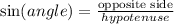
Considering angle D, the opposite side is FE, then:

`\begin{gathered} \sin D=(FE)/(DE) \\ \sin D=(20)/(29) \end{gathered}`

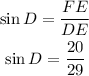
Considering angle E, the opposite side is DF, then:

`\begin{gathered} \sin E=(DF)/(DE) \\ \sin E=(21)/(29) \end{gathered}`

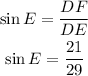
Cosine formula

`\cos (angle)=\frac{\text{adjacent side}}{hypotenuse}`

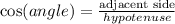
Considering angle D, the adjacent side is DF, then:

`\begin{gathered} \cos D=(DF)/(DE) \\ \cos D=(21)/(29) \end{gathered}`

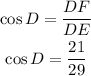
Considering angle E, the adjacent side is FE, then:

`\begin{gathered} \cos E=(FE)/(DE) \\ \cos E=(20)/(29) \end{gathered}`

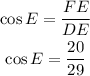
Tangent formula

`\tan (angle)=\frac{\text{opposite side}}{adjacent\text{ side}}`

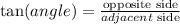
Considering angle D, the opposite side is FE and the adjacent side is DF, then:

`\begin{gathered} \tan D=(FE)/(DF) \\ \tan D=(20)/(21) \end{gathered}`

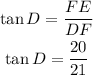
Considering angle E, the opposite side is DF and the adjacent side is FE, then:

`\begin{gathered} \tan E=(DF)/(FE) \\ \tan E=(21)/(20) \end{gathered}`