Question

A person's vision may be improved significantly by having the cornea reshaped with a laser beam, in a procedure known as photorefractive keratectomy. The excimer laser used in these treatments produces ultraviolet light with a wavelength of 182 \rm nm.What is the difference in energy between the two levels that participate in stimulated emission in the excimer laser?How many photons from this laser are required to deliver an energy of 1.28×10−13 to the cornea?

Answer 1

Given data

*The given wavelength of the ultraviolet light is

`\lambda=182nm=182*10^(-9)\text{ m}`

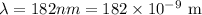
*The given total energy is E_t = 1.28 × 10^-13 J

The formula for the difference in energy between the two levels that participate in stimulated emission in the excimer laser is given as

`\Delta E=(hc)/(\lambda)`

*Here h = 6.626 × 10^-34 J.s is the Planck's constant.

*Here c = 3.0 × 10^8 m/s is the speed of the light.

Substitute the known values in the above expression as

`\begin{gathered} \Delta E=((6.626*10^(-34))(3.0*10^8))/((182*10^(-9))) \\ =0.109*10^(-17)\text{ J} \end{gathered}`

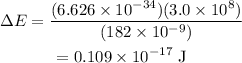
Hence, the difference in energy between the two levels that participate in stimulated emission in the excimer laser is 0.109 × 10^-17 J

The number of photons from this laser is required to deliver energy is calculated as

`\begin{gathered} E_t=n\Delta E \\ n=(E_t)/(\Delta E) \\ =(1.28*10^(-13))/(0.109*10^(-17)) \\ =\text{1}.17*10^5\text{ photons} \end{gathered}`

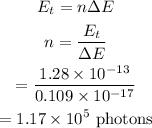
Hence, the number of photons from this laser is required to deliver energy is n = 1.17 × 10^5 photons