Question

A chemist has 20% and 50% solutions of acid available. How many liters of each solution should be mixed to obtain 105 liters of 22% acid solution?

Answer 1

Step-by-step explanation:

let the amount of solution used for the 20% concentration = x

let the amount of solution used for the 50% concentration = y

We want to obtain a mixture of 105 liters

amount for 20% + amount for the 50% = 105 liters

x + y = 105 ....(1)

The concentration for the mixture = 22%

20% (amount used) + 50% (amount used) = 105 (22% acid solution)

0.20(x) + 0.50 (y) = 105(0.22)

0.2x + 0.5y = 23.1 ....(2)

Using substitution method:

From equation 1, we can make x the subject of formula

x = 105 - y

we will substitute for x in equation (2):

`\begin{gathered} 0.2(105\text{ - y) + 0.5y = 23.1} \\ 21\text{ - 0.2y + 0.5y = 23.1} \\ 21\text{ + 0.3y = 23.1} \\ 0.3y\text{ = 23.1 - 21} \\ 0.3y\text{ = 2.1} \end{gathered}`
`\begin{gathered} \text{divide both sides by 0.3:} \\ (0.3y)/(0.3)\text{ = }(2.1)/(0.3) \\ y\text{ = 7} \end{gathered}`

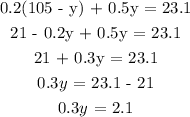
substitute for y in equation (1):

`\begin{gathered} x\text{ + 7 = 105} \\ \text{subtract 7 from both sides:} \\ x\text{ + 7 - 7 = 105 - 7} \\ x\text{ = 98} \end{gathered}`

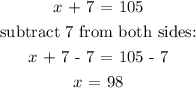
Hence, 98 liters of 20% solution and 7 liters of 50% solution should be mixed