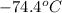Answer : The new temperature will be,
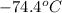
Explanation :
Charles' Law : This law states that volume of gas is directly proportional to the temperature of the gas at constant pressure and number of moles.
 (At constant pressure and number of moles)
(At constant pressure and number of moles)
or,
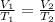
where,
 = initial volume of gas =
= initial volume of gas =
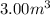
 = final volume of gas =
= final volume of gas =
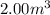
 = initial temperature of gas =
= initial temperature of gas =
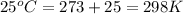
 = final temperature of gas = ?
= final temperature of gas = ?
Now put all the given values in the above formula, we get the final temperature of gas.

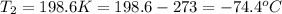
conversion used :
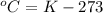
Therefore, the temperature will be,