Question

If the ratio of the corresponding side lengths of two similar polygons is 6:11, what is the ratio of their areas?

A.
6:11
B.
12:11
C.
36:11
D.
36:121

Answer 1

Answer: D. 36:121

Explanation:

Given: The ratio of the corresponding side lengths of two similar polygons is

`r_1:r-2=6:11\\\\\text{OR}\\\\(r_1)/(r_2)=(6)/(11)`

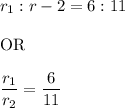
Since we know that the area of any polygon required two dimensions, therefore, the ratio of the surface area of the polygons is given by :-

`(S.A._1)/(S.A._2)=(r_1^2)/(r_2^2)=(6^2)/(11^2)=(36)/(121)`

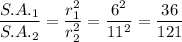
Hence, the ratio of their areas= 36:121

Answer 2

the ratio of areas is just the square of ratio of sides,
so
(6:11)^2 = 6^2 : 11^2 = 36:121