Question

Use the midpoint formula method to find the equation of the perpendicular bisector of the linesegment whose endpoints are (0, 0) and (8. 4). Write the equation in general form.

Answer 1

Given the points (0,0) and (8,4)

The midpoint will be the point M, which can be calculated as following :

`M=((0,0)+(8,4))/(2)=((8,4))/(2)=(4,2)`

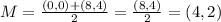
The slope of the line segment with the endpoints (0,0) and (8,4) will be :

`slope=(rise)/(run)=(y_2-y_1)/(x_2-x_1)=(4-0)/(8-0)=(4)/(8)=(1)/(2)`

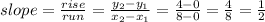
So, the slope of the perpendicular to the given line segment = -2

So, the required line have a slope of -2 and passing through the point ( 4 , 2 )

The slope - point form of the line will be :

`(y-2)=-2(x-4)`

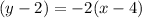
And the general form will be :

`\begin{gathered} y-2=-2x+8 \\ y=-2x+8+2 \\ \\ y=-2x+10 \end{gathered}`