SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given data values

STEP 2: Write the equation
The equation of a hyperbola is given as:
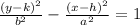
where (h,k) is the center, a and b are the lengths of the semi-major and the semi-minor axes.
STEP 3: Explain the given data
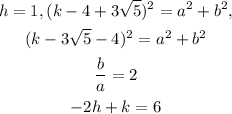
STEP 4: Find the values of h,k,a and b
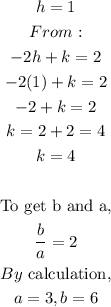
STEP 5: Get the equation of the hyperbola
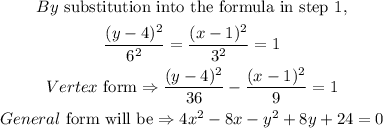
Hence, the equation of the hyperbola will be:
General form:
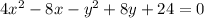
The vertex form is given as:
