Question

Part A: Which of the functions represents an exponential function? What is the common ratio of that function?Part B: What is the average rate of change for the function h(x) over the interval 2 ≤ x ≤ 4?

Answer 1

(a)f(x), Common Ratio = 1/4

(b)-12

Explanation:

Part A

From the functions on the table, the function that represents an exponential function is f(x).

The common ratio of f(x) is derived below:

`\begin{gathered} 512*(1)/(4)=128 \\ 128*(1)/(4)=32 \\ 32*(1)/(4)=8 \\ 8*(1)/(4)=2 \end{gathered}`

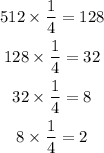
The common ratio is 1/4.

Part B

We want to find the average rate of change for the function h(x) over the interval 2 ≤ x ≤ 4.

From the table:

• When x=4, h(x)=9: h(4) = 9

,

• When x=2, h(x)=33: h(2) = 33

`\begin{gathered} \text{ Average Rate of Change}=(h(4)-h(2))/(4-2) \\ =(9-33)/(2) \\ =-(24)/(2) \\ =-12 \end{gathered}`

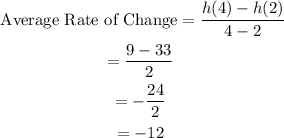
The average rate of change for h(x) over the interval 2 ≤ x ≤ 4 is -12.