Step-by-step explanation
The length of an arc is given by the formula
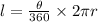
where θ is the angle at the center of the circle that subtends the arc.
If the central angle has a measure of π/2(90°), then the length of the arc will be one-fourth of the total, while if the measure of the angle is π(180°), then the length of the arc will be half of the total.
Similarly, if the measure of the angle is 3π/4, then the length of the arc will be three-fourth of the total, while if the measure of the angle is 2π(360°), then the length of the arc will be 2πr.
Answer: Option C