Question

A student factors 3x2 – 12 to the following. 3(x2 – 4) Which statement about 3(x2 – 4) is true? A. The expression is equivalent, and it is completely factored. / B.The expression is equivalent, but it is not completely factored./ C. The expression is not equivalent, but it is completely factored./ D.The expression is not equivalent, and it is not completely factored.

Answer 1

B. The expression is equivalent but not completely factored.

You can continue to factor

3 (x^2-4) =

3 (x+2)(x-2)

Answer 2

Option B is correct that is the expression is equivalent, but it is not completely factored.

Explanation:

We have given an expression

`3x^2-12`

when we take the common factor out which is 3 from the expression we will get

`3(x^2-4)`

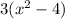
This expression is equivalent but is not completely factored because the term

`(x^2-4)\text{can be further factored as}(x-2)\text{and}(x+2)\text{from the formula}a^2-b^2=(a+b)(a-b)`

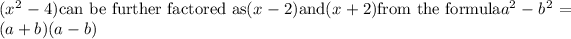
Hence, Option B is correct.

Option C and D are discarded because given factor is equivalent

Option A is discarded because expression is not completely factored.