Question

Given f(x)=3x+5 describe how the graph of g compares with the graph of f. g(x)=3(0.1)+5

Answer 1

The given function f(x) is:

`f(x)=3x+5`

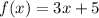
And the other given function g(x) is:

`g(x)=3(0.1x)+5`

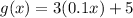
g(x) in comparison with f(x) has the next transformation:

1. g(x)=f(bx): g(x)=3(0.1x)+5. This is a horizontal stretch: the x-coordinates will change as:

`(x,y)\rightarrow((x)/(0.1),y)`

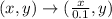
This is the graph of both functions:

The red-one is f(x) and the blue-one is g(x).

Then for example when the coordinates of f(x) are (1,8) for g(x) the coordinates will be:

`((1)/(0.01),8)=(10,8)`

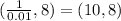
Then, the slope of f(x) has a greater value than the slope of g(x), since the change on the x-axis is bigger in the g(x) graph for the.