Question

a person standing close to the edge on the top of a 96 foot building throws a ball vertically upwards. the quadratic function h(t)= -16t^2 + 80t + 96 models the balls height about the ground, h(t) in feet, t seconds after it was thrown. what's the maximum height of the ball?

Answer 1

Let's compute h'(t) to find its maximum:

`h^(\prime)(t)=-32t+80`

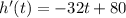
In order to find its maximum, we equal it to 0, solve for t and replace the value we get in h(t):

`-32t+80=0`

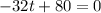
From this

`t=(5)/(2)`

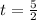
Substituting in h(t) we get:

`-16((5)/(2)^{})^2+80((5)/(2))+96=196`

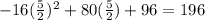
Thus the maximum height of the ball will be 196 feet.

In order to know how many seconds will pass until the ball hits the ground, we must solve h(t)=0

`-16t^2+80t+96=0`

From this we get:

`t_1=-1,t_2=6`

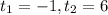
Since it doesn't make sense for the ball to hit the ground in negatve time, the ball will hit the ground after 6 seconds.