Question

The sm, S, et me faktin vamos en urbantie sunce is even they sa-(23* ap), in which an, is the thesis tom and son is the one team. The sum op of the formterms of gettistence is given by sein which is the first form and is the common ratio 4+1) Determine whether the following serveraltimdi o pomie Then use the 20te fonda to find S, the sum of the first tohtorms3.6.9.12Dermine whether the summer is the oneware Chores the emet uw bowSem

Answer 1

We have the sequence 3, 6, 9, 12.

We can prove that this sequence is not geometric by calculating the ratios a2/a1 and compare it to a3/a2. If the ratios are not equal, the sequence is not geometric: there is no common ratio in the sequence.

`\begin{gathered} (a_2)/(a_1)=(6)/(3)=2 \\ (a_3)/(a_2)=(9)/(6)=1.5 \\ (a_2)/(a_1)\\eq(a_3)/(a_2)\Rightarrow\text{ not a geometric sequence} \end{gathered}`

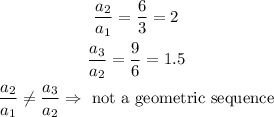
We can prove it is a arithmetic sequence because it has a common difference d=3 between consecutive terms:

`\begin{gathered} a_2=a_1+3=3+3=6 \\ a_3=a_2+3=6+3=9 \end{gathered}`

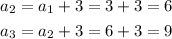
Now, we have to calculate the sum.

We start by calculating a10, using the explicit function for an arithmetic sequence:

`a_(10)=f(10)=3+3\cdot(10-1)=3+3\cdot9=3+27=30`

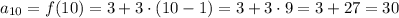
Then, we apply the formula given for the sum of n terms:

`\begin{gathered} S=(n)/(2)(a_1+a_n) \\ S_(10)=(10)/(2)(3+30)=5\cdot33=165 \end{gathered}`

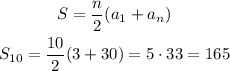
Answer:

The sequence is arithmetic.

The sum of the first 10 terms is S10=165.