Question

Score: 11.33/20 11/20 answeredQuestion 20< >The annual rainfall in a certain region is approximately normally distributed with mean 42.3 inches andstandard deviation 5.2 inches. Round answers to the nearest tenth of a percent.a) What percentage of years will have an annual rainfall of less than 44 inches?

Answer 1

Given

The mean of the average rainfall is 42.3 inches.

The standard deviation is 5.2 inches.

To find:

a) What percentage of years will have an annual rainfall of less than 44 inches?

b) What percentage of years will have an annual rainfall of more than 40 inches?

c) What percentage of years will have an annual rainfall of between 39 inches and 43 inches?

Step-by-step explanation:

It is given that,

The mean is 42.3 inches.

The standard deviation is 5.2 inches.

a) Consider the value of X as 44.

Then,

`\begin{gathered} z=(X-\mu)/(\sigma) \\ =(44-42.3)/(5.2) \\ =(1.7)/(5.2) \\ =0.3269 \end{gathered}`

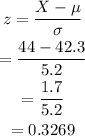
Therefore,

`\begin{gathered} P(X<44)=P(z<0.3269) \\ =0.62814 \end{gathered}`

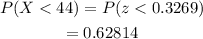
Hence, the percentage of years when p(X<44) is,

`\begin{gathered} \%=0.62814*100 \\ =62.814\% \end{gathered}`

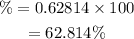
b) Also,