Question

An object experiences a constant acceleration of 2 m/s/s along the -x-axis for 2.7s, attaining a velocity of 18.m/s in a direction 47 degree from the +x-axis. Calculate the magnitude of the initial velocity vector of the object.

Answer 1

We know that the final velocity of the object is 18 m/s in a direction of 47° from the x-axis; this means that the final velocity as vector is:

`\begin{gathered} \vec{v}=\langle18\cos 47,18\sin 47\rangle \\ =\langle12.28,13.16\rangle \end{gathered}`

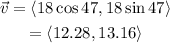
Now, since the acceleration is along the x-axis this means the the y-component of the initial velocity remains constant; hence the y-component of the final velocity is the same as the y-component of the initial velocity. This also means that the x-component is the only one that changes; since the acceleration is constant throught the 2.7 seconds we can use the formula:

`a=(v_f-v_0)/(t)`

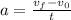
To find the x-component of the initial velocity:

`\begin{gathered} -2=(12.28-v_0)/(2.7) \\ -2(2.7)=12.28-v_0 \\ v_0=12.28+2(2.7) \\ v_0=17.68 \end{gathered}`

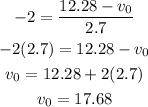
Therefore the initial velocity is:

`\vec{v}_0=\langle17.68,13.16\rangle`

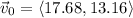
Its magnitude is:

`\begin{gathered} v_0=\sqrt[]{(17.68)^2+(13.16)^2} \\ v_0=22.04 \end{gathered}`

Therefore the magnitude of the initial velocity is 22.04 m/s.