Part A:
Vertical Angle Theorem states that two opposite vertical angles formed when two lines intersect each other are congruent to each other.
∠7 and ∠8 are a pair of vertical angles. Therefore, they are congruent.
Part B:
By vertical angle theorem, the adjacent angles to ∠7 and ∠8 are also congruent. Equate the two unknown angles, so that we can solve for y.
Part C:
Solving for y, we have the following:
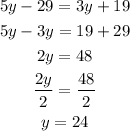
Since ∠7 or ∠8 are linear pairs with (5y - 29) and (3y + 19), they are suppementary which means that
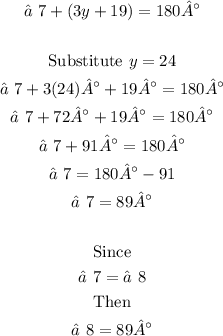
Therefore, the measures of ∠7 and ∠8 is 89°.