10. We have to compare the central angles and the arcs of the original wheel and its replica.
If we divide a circumference in 32 sectors, the central angle will be:
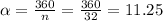
where n is the number of sectors.
We can see that this angle is independent of the radius of the circumference, so we can conclude that it will be the same for the original wheel and for its replica.
In the case of the arc length, it will depend not only on the central angle but also the radius.
In this case, the arc angle will be proportional to the radius of the wheel and therefore will be different for the original wheel and the replica.
We can express the arc length between two consecutive cars as:
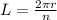
This can be think of as: each arc length is 1/32 of the full circumference, which has a length of 2π times the radius.
11. If the center of the wheel is at (0,0) and the radius is 120 m. we can write an equation of the circumference as:
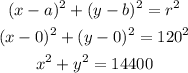
and we can represent it as:
Answer:
10. The central angle will be equal for the original wheel and for its replica.
The arc length will be proportional to the radius of the wheel, so it will be different for the original wheel and its replica.
11. The equation is x² + y² = 14400.